This article describes a straightforward implementation of binary triangle trees (BTT) to produce terrain geometry in Macromedia Director with 3D Lingo. Part of the code is based on a 1999 article by Seumas McNally describing BTT spliting and linking logic (see reference 1)

Binary Triangle Trees

A Binary Triangle Tree is a data structure describing the successive splitting of a root triangle via a recursive process, down to a defined level of detail. In such a structure, each triangle or node keeps track of its two children, if they exist (see figure 1)

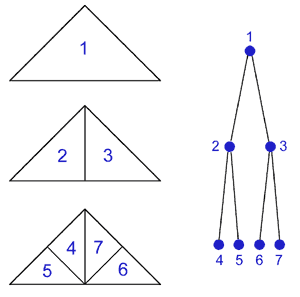
figure 1

When using this process to approximate a heightfield (or any continuous surface) it is necessary to avoid introducing 'cracks' or 'seams' in the geometry that arise when neighboring triangles are of different levels of detail. To do so, each triangle in the tree must also keep track of its three neighbors - left, right and bottom - if they exist.

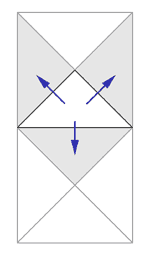
figure 2

In a split operation a 'seam' can appear at the middle of the hypotenuse where a new vertice is introduced to support the children. To avoid such gaps, the process must make sure that the bottom neighbor, which shares the hypotenuse, is brought to the same level of detail.

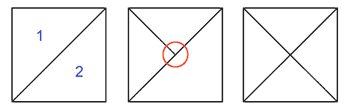
figure 3

In a 'normal' split where the bottom neighbor is already at the same level, both triangles are split, making a 'diamond' figure (see figure 3)

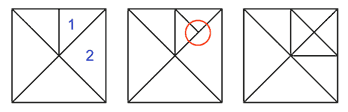
figure 4

If the bottom neighbor is of a lower level of detail it must be forced to split before the 'normal' split can occur (see figure 4)

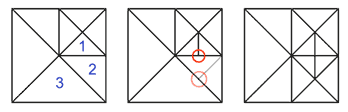
figure 5

These forced splits can (and must) propagate in a chain reaction to lower levels of detail if necessary (see figure 5)

At each step in the splitting process, links to and from all three neighbors must be properly maintained.

To split or not to split ?

When building a triangle tree for a terrain, several criteria can come into play to decide how far a branch should split. An important consideration is how close to the reference heightfield is a triangle. If it accurately represents the underlying terrain it does not need further splitting and the optimal level of detail has been reached. Another consideration is whether a particular triangle is close to, or far away from, the camera - or whether it is in the line of sight. In fact, any clever formula can be elaborated to decide how 'deep' the tree should grow depending on the application goal and constraints.

In the following lingo example, a 'variance' is recursively computed for each triangle, based on the maximum difference between the altitude of the interpolated point at the middle of the hypotenuse and the real altitude provided by the heightfield. This 'variance' takes into account a particular triangle and all its potential children down to the finest level of detail to make sure no small 'bump' is overlooked in the process.

By defining a threshold for split, based on triangle variance, you can control the level of detail of the resulting terrain and the amount of polygons involved.

Dual Triangle Tree

When it comes to render a square terrain, it is appropriate to grow not one triangular tree but two trees from two roots triangles covering the whole area. Since the two starting nodes are cross-linked as bottom neighbors, the two trees will grow happily as one.

Pseudo code

Here is the pseudo code to build a terrain with BTT:

• create vertice and texture coordinate list for all data points in the heightfield
• build the terrain tree [1] down to a defined variance (level of detail - 0 is best fit)
• create face list according to the tree (triangles with no childs)
• create texture and shader
• create model

1: Building the terrain tree:

• Initialize the tree with two big triangles covering the whole terrain
• build face [2] one
• build face [2] two

2: Building a face (recursive):

• if it already has childrens (from propagated splits) then build [2] left child and right child
• othewise
  • if the triangle variance is higher then the maximum allowed
    • split [3] this face
    • build [2] the resulting left and right child

3: Splitting a face (recursive):

• if bottom neighbour is not symetric (different level of detail) then split [3] it first
• 'really' split [4] bottom neighbour and the current face (make diamond)
• cross-link their childs

4: and finaly the 'real' split (split2)

• create the two childs
• keep track of links with and from neighbours

There are two recursive methods. Building a face [2] essentialy 'digs' until no triangle has a variance higher than that allowed. Splitting a face [3] also splits bottom neighbours if necessary, in a chain reaction, to avoid 'cracks' or 'seams' in the mesh.

Note that the face building (or 'digging') [2] checks if the current face already has children. This case arises when a face that has not been built yet has previously been forced to split to adjust to neighboring triangles.

The vertice and texture coordinate lists cover all data points of the heightfield. However many of them will not be used in the final mesh (this is the whole idea). A more optimised process would shorten (or defragment) the two lists.

Lingo Code

In this Lingo example the triangle tree is implemented as a list of triangles, each triangle being defined as a property list:

[#v1:int, #v2:int, #v3:int, #lc:int, #rc:int, #ln:int, #rn:int, #bn:int]

where

• v1, v2 and v3 are references to the three vertices involved in the vertice list
• lc and rc if not null are references to the left child and the right child in the tree list
• ln, rn and bn if not null are references to the left, right and bottom neighbours in the tree list

The heightfield is a 129 by 129 pixel grayscale elevation map. Any map with sides of a power of two plus one will do (257, 513, 1025...). Ground texture comes from a square bitmap that can be any size.

Play .dcr (18k) or Download .dir (200k)
Terrain texture as been kept very small to keep download size minimal. It realy looks better with a large bitmap !

Going further

The Binary Triangle Tree approach has been used in real-time algorythms where the terrain level of detail evolves according to the camera motion for example. In that situation, triangles are constantly split or merged to maintain a target polygon count and perceived accuracy (see reference 2. ROAM).

I hope this helps some of you get started with the wonderful world of terrains. The 'terrain handler' Lingo code should really be object oriented with methods and properties instead of globals... sorry about that :)

References

1. Binary Triangle Trees and Terrain Tessellation by Seumas McNally, 1999
http://www.gamedev.net/reference/articles/article806.asp

2. ROAMing Terrain: Real-time Optimally Adapting Meshes by Mark Duchaineau et al. 1997
http://www.cognigraph.com/ROAM_homepage/index.html

3. Terrain Level Of Detail Published Papers, a comprehensive list at the Virtual Terrain Project
http://www.vterrain.org/LOD/Papers/

-
Patrick Murris, Montreal
November 2003